Instant Runoff Voting in Oakland
Earlier this month, Oakland elected its first Asian American to the less than coveted role of city mayor. Jean Quan emerged victorious this election day, although at one point she was trailing her opponent by 11 percentage points. Understood in context, however, her victory is perhaps less surprising - rather than winning by Plurality, Quan won under Oakland's Instant Runoff Voting system.

I don't know much about Oakland politics, but this picture sure makes her look ready for business.
What's the difference? For most elections in the United States, voters are instructed to cast their vote for the individual who they would most like to see get elected. These votes are tallied, and the one with the most votes is declared the winner. In contrast, the Instant Runoff Voting system asks voters to rank several candidates at once - this extra information is used to automatically determine the outcome of a runoff if no candidate has a majority of first choice votes.
For a more detailed explanation, let's use this mayoral race as an example. There were 10 candidates on the ballot for mayor, and voters were allowed to choose their top three (ranking them 1st, 2nd, and 3rd). Voters were also allowed to write in a candidate if they so chose. If, after tallying the votes, no candidate has a majority, then the candidate with the FEWEST number of votes is eliminated, and the voters who voted for that eliminated candidate now have their second place votes distributed among the remaining candidates. This process continues until one candidate has a majority of the votes (if a voter's first, second, and third choices are eliminated, the vote is considered 'exhausted,' i.e. the vote does not contribute to any of the remaining candidates' tallies, and the percentage of the vote that a candidate has earned is given as a proportion of the votes excluding the exhausted votes).
How did this shake out for Oaktown? The Alameda County website has posted detailed results. Because of the large number of candidates, the process described above had to be applied a number of times. Let me simplify things a bit and look only at the last few rounds.
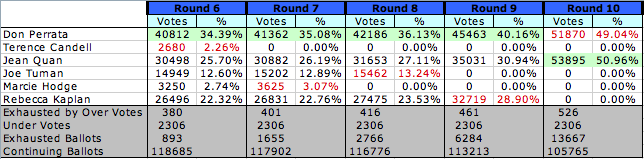
Here's a simplified version of the data you can find from the link above.
The data shows, for example, that in Round 6, Terence Candell had the fewest number of votes. Therefore, he was eliminated from the running, and his 2,680 votes were distributed among the remaining candidates, according to the preferences indicated on the ballot. In the next round, Marcie Hodge had the fewest number of votes, and so she was eliminated and her votes were distributed among the remaining candidates. And so on. Eventually, Jean Quan emerged victorious, despite the fact that Don Perrata was the leader in every other round. This is probably due in no small part to the combined strategy of Kaplan and Quan - according to this article, the two joined forces and asked voters to place them in first and second place on the ballot.
In a sense, this voting system may seem better than the usual system - after all, by ranking 3 candidates, it would seem as though the voter's true preferences would be more accurately reflected. However, for anyone who has read about the mathematics of voting (a subject I've touched on before), this statement might seem dubious. Forgetting for a moment the practical disadvantages (the costs associated with implementing such a system, for example), Instant Runoff Voting is still a ranked preference system, i.e. one in which voters can rank candidates in some order, but can't supply any more detailed information (e.g., by how much a voter prefers one candidate over another). As such, this voting system falls under the umbrella of Arrow's Impossibility Theorem, which essentially tells us that this system lacks some feature that we would want out of a good voting system. In this case, Instant Runoff voting isn't monotonic - in other words, ranking a candidate higher on your ballot can actually hurt that candidate's chances of winning (versus an alternative in which you ranked that candidate lower).
If cities are going to change the way they elect people, I would instead encourage them to consider Range Voting (as I've mentioned before). Here's a brief summary comparing Range Voting to Instant Runoff Voting. While Range Voting isn't immune to tactical voting in a field with more than 3 candidates, it has a number of both practical and mathematical advantages over Instant Runoff Voting (or any ranked preference voting system, for that matter). For example, Range Voting is monotonic, would be less expensive to implement, and would most likely decrease voter error.
Regardless of your opinion of the rules, Quan won by those rules, so kudos to her. But if you're an Oakland resident unhappy with the process, I'd encourage you to look into Range Voting as a better alternative than backsliding to the plurality system used in most of the country.
(Hat tip to mother for linking me here.)
Psst ... did you know I have a brand new website full of interactive stories? You can check it out here!
comments powered by Disqus
