Hello, World!
Hi there! How are you? It's been a while. You're looking good, is that a new shirt?
Well, enough about you. Let's talk about Math Goes Pop. As you may have noticed, the output lately has been - to put it kindly - a little slow. Part of the reason for this is that I've been spending some of my free time retooling the blog. As a Tau Day gift, the fruits of my labors are now laid bare here before you.
Math Goes Pop has been rebuilt from the ground up. Aesthetics aside, the site is much the same as it was before, but hopefully feels a little cleaner and works a little better. I'd also like to tip my hat to Mira Gomha, who designed the new logo. If you want to see more of her work, you can check out her portfolio or give her a shout on Twitter.
Now that Math Goes Pop has a shiny new coat of digital paint, you can expect to see musings from me on a somewhat more regular basis. For now, I'll just leave you with a small puzzler that came to mind as I was migrating all the old posts from...
Give it Away, Give it Away, Give it Away Later
For hockey fans, summer is a quiet time of year. I've never followed the sport that closely, but with the Kings having recently won the Stanley Cup for the second time in three years, I'm reminded of a curious incident that I witnessed during the only NHL game I've ever been to.
A friend of mine received free tickets to a Kings game when I was living in LA several years ago. He invited my now-wife and me along, and the price was certainly right, so four of us went to the Staples center one Saturday afternoon.
I don't remember much about the game (though I do recall that the Kings emerged victorious). What I remember most vividly was that during one of the breaks between periods, a new car was brought onto the ice and there was a contest to give that car away. Sort of like what happens in this video, but the rules were a little different:
In the game I attended, six contestants were given a key to a new car, but they were told that only one key would start the vehicle. One at a...
Keeping it Real: An Addendum
Last week, Dan Meyer invited the folks at Mathalicious to opine on the meaning of the phrase "real-world," not as it applies to MTV shows (though that would make for a great conversation), but as it applies to questions asked of students in a math classroom. This week, we responded, continuing what I believe to be an important and interesting discussion about the nature of what we mean when we demand that mathematics be made more "real" for our students.
Most of my thoughts on the subject are encapsulated in the Mathalicious response. (Both articles come highly recommended, and what I say below may not make much sense if you haven't read them first.) The conversation got me thinking, though, and so I'd like to offer my own personal aside/addendum.
When I began writing in this corner of the internet in the summer of 2008, my goal was simply to talk about mathematical ideas in a way that was accessible for a general audience (and in particular, an audience that didn't necessarily think...
It's Not Complicated. Or is it?
Though I am hardly AT&T's biggest fan, I can't help but be charmed by their "It's Not Complicated" ad campaign. Each ad features a dapper looking man asking softball questions to a group of young children. Though the ads are meant to elicit mostly meaningless platitudes that AT&T then spins as selling points (e.g. "Faster is Better"), the children's answers and the gentleman's reactions make the ad-watching experience just a little bit more bearable.
In one of the campaign's more recent ads, however, I was disappointed to see a teachable moment go to waste. I suppose this is what happens when you have a cell phone company spokesman in a room full of children instead of an actual teacher. (Though to be fair, the math involved isn't really suitable for elementary school.)
Here's the ad:
In case you don't have time to watch cell phone commercials, here's a transcript of their conversation.
AT&T Guy: What's the biggest number you can think of?
Girl 1: A trillion billion zillion...
Down with Plurality!
Hi friends,
As some of you may know, in general I don't hold our country's voting methods in very high regard. Think about the way we vote for president, for instance. Aside from not asking voters to state any preferences at all, it's difficult to do worse than our current system: we can only show our support for a single candidate, when in fact our preferences may be more nuanced. Moreover, since we can only vote for a single candidate, there's little incentive to vote for our favorite one, unless our favorite happens to be a front-runner. This is known all across the universe, as evidenced by the Presidential runs of Kang and Kodos:
Even worse, a third party candidate who garners a decent amount of support may end up hurting his own party and parties more closely aligned to it by acting as a "spoiler." Of course, the most well-known example of this is Ralph Nader, who many people believe cost Al Gore the 2000 election (for more on the spoiler effect, see here).
For all these...
Mathalicious Post: Most Expensive. Collectibles. Ever.
Hey y'all. My most recent post on the Mathalicious blog has been live for a while, but in case you missed it, I'd encourage you to go check it out! Consider it a Simpsons themed cautionary tale for collectors on a budget. Here's a sample:
One of the more recent trends in the world of Simpsons memorabilia is the advent of the Mini-Figure collections, produced by Kidrobot. Each series (there have been two so far) consists of around 25 small Simpsons figures, each with his or her own accessories. The figures cost around $10 each ($9.95, to be precise), so an avid collector would need to spend something like $250 to complete each of the two collections, right?Well, not quite. When you buy one of these figures, you have no idea which one you’ll get, because the box containing the figure doesn’t indicate what’s inside. All you know are the probabilities for each figure, and even those are sometimes missing...
Given this information, here’s a natural question: how many of these boxes...
Math in Books: The Universe in Zero Words
I recently had the pleasure of reading The Universe in Zero Words: The Story of Mathematics as Told through Equations. Written by Dr. Dana Mackenzie, the book frames mathematical history in terms of some of the most important equations ever discovered. While writing about equations for a general audience can be a dangerous game, Dr. Mackenzie tackles mathematical notation head on. If the sight of an equation causes a chill to run down your spine, fear not; the book eases you in with the very simplest of equations (we're talking 1 + 1 = 2 here) and guides you gently through a history of mathematics, from antiquity to present day.
Of course, as you move closer to the present, the equations get a little more sophisticated. Even so, Dr. Mackenzie does his best to ground the equations to something relatable to a wide audience (and by and large, he's quite successful). For instance, he uses whales as a way to talk about non-Euclidean geometry: you can read more about this example
Mathalicious Post: Doubling Down
My latest entry on the Mathalicious blog riffs on the strategy of doubling down, using the film Swingers as a jumping off point. Here's a preview:
“You always double down on 11, baby.” Sage advice from Vince Vaughn’s character in the 1996 film Swingers. At one point in the film, Trent (played by Vaughn) and Mike (played by Jon Favreau) make an impromptu trip to Las Vegas, and Mike ends up completely out of his depths at a high-stakes blackjack table...Mike receives a six and a five, giving him a total of eleven. Trent urges him to double down, and indeed, this seems like good advice. After all, in a deck of 52 cards, 16 of them have a value of 10 – that’s over 30%! Always doubling down on eleven is also consistent with the basic blackjack strategy popularized by Edward O. Thorp in his book Beat the Dealer. From a mathematical standpoint, Trent is right. You should always double down on eleven.Interested in the rest of the story? Click here!
Mathalicious Post: To Foul Or Not To Foul
Greetings, mathletes. As some of you know, I've recently joined the crew of good folks at Mathalicious. Consequently, the blog work here is in a bit of a transition, but don't worry! I will still be around, though the focus may shift somewhat.
How Math Goes Pop! will be changing is the subject for another post. One thing's for sure, though: I'll be contributing to the Mathalicious blog regularly. My first post, on whether or not it makes sense to foul the opposing team at the buzzer in a close basketball game, went live last week. Here's a small sample:
A three point shot by Sundiata Gaines turned a two-point loss for the Jazz into a one-point win. No doubt that’s a tough defeat for Cavs fans and players alike, but in such a situation, there’s really nothing the defense could’ve done to change the outcome.Or is there? What if, instead of letting Gaines take the shot, the defense had fouled him? Could that have increased the Cavs’ likelihood of maintaining their lead? If Gaines...
Pi(e) Mathematics
Gentle reader, I apologize for the dearth of updates recently. But with a new month comes new opportunity for mathematical investigation, so let's dive right in!
In keeping with my summertime theme of mathematics and food (see e.g. here and here), I'd like to share with you a story about a recent dinner I shared with my better half. After a day spent apartment hunting, we decided to treat ourselves to a dinner out.
Everything we learned about treating ourselves we learned from Parks and Recreation.
In keeping with the theme of treating ourselves, we ordered two desserts at the end of the night, and both looked quite delicious. We agreed to each eat half of one dessert and then trade for the second half. One was in the general pie family of desserts.
Given a slice of pie, the most natural way to divide it in half is to bisect the angle formed at the end of the slice.
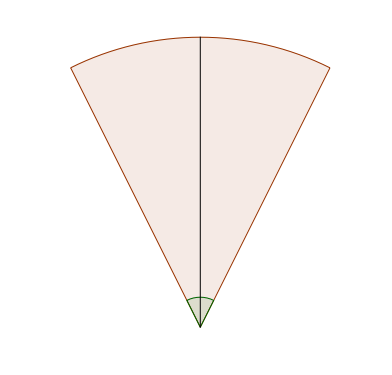
One slice of pie, cut in half by bisecting the green angle.
To cut a slice of pie in this manner, one generally...
Page 2 of 20


