A New Birthday Problem
Last week, Slashdot posted an interesting link to a problem posed at the most recent Gathering 4 Gardner, a mathematical (or perhaps I should say mathemagical) convention created in honor of the late Martin Gardner. The question, posed by Gary Foshee, is as follows: you have a friend with two children, one of whom is a boy born on a Tuesday. What is the probability that the other child is a boy?
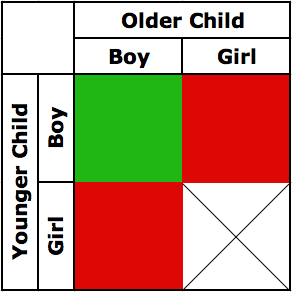
Forget about the Tuesday fact for a moment - if you have a friend with two children, one of whom is a boy, what is the probability that the other child is a boy? You might expect that the answer should be 50%, since the sex of one child shouldn't affect the sex of the other. But this is not quite right, because you're not told whether the boy is the older or younger child.
There are only four possibilities when one has two children, so the situation is easy to analyze. With two kids, the four possibilities are boy boy, boy girl, girl boy, and girl girl. If you know that one of the kids is a boy, this eliminates girl girl from the list of potential combinations, leaving us with the three outcomes boy boy, boy girl, and girl boy. Of these three outcomes, we see that only the first has two boys, and so we conclude that the probability of the second child being a boy is 1/3, NOT 1/2!
There's another way to answer this question, one that generalizes nicely to the more complicated question asked by Foshee. There are two cases to consider: either the boy you know about is the younger child, or the older child. If the boy you know about is the younger child, there are two possibilities for the older child (girl or boy). Similarly, if the boy you know about is the older child, there are two possibilities for the younger child (girl or boy). This gives four outcomes, but you have counted the boy boy outcome twice. In other words, we see there are only three distinct outcomes, and only one of them has two boys, so again we see that the probability is 1/3.
Now let's return to the original question. Again, it seems like the fact that the boy was born on a Tuesday shouldn't matter, but if we do the same analysis as above, we'll see that this is not the case. The information about the day does make the number of outcomes larger, however, so it's easier to get mixed up.
As before, let's split into two cases, depending on whether the Tuesday boy is younger or older. If the younger child is the Tuesday boy, then there are 14 possible outcomes for the older child, since there are 2 choices for the sex of the child and 7 choices for the day of the week on which the child was born. Similarly, if the older child is the Tuesday boy, there are once again 14 possible outcomes for the younger child. However, notice that we have counted the outcome of two boys both born on Tuesday twice, just as we counted the outcome of two boys twice in the simpler problem. Correcting for this double counting, we see that there are 14 + 14 - 1 = 27 possible outcomes. Of these outcomes, 13 of them correspond to having a two boys - if the younger child is the Tuesday boy, there are 7 possible outcomes that will give us two boys, and if the older child is the Tuesday boy, there are again 7 possible outcomes. As before, though, we've counted both children being Tuesday boys twice, so we subtract 1 to correct for this double-counting, which leaves us with a total of 7 + 7 - 1 = 13 desired outcomes. This means that the probability of the second child being a boy is 13/27. While still not equal to 1/2, this is much closer to 1/2 than 1/3.
Much like the Monty Hall problem, however, one can understand the mathematical reasoning behind this problem and still have trouble with the intuition. After all, why should the day on which a child was born have any bearing on the sex of the other child? On the face of it, the solution to this problem doesn't make any sense. One way to try and marry this solution to our intuition is to assign some numbers and explore the data, seeing where our intuition diverges from this picture.
Suppose we take a survey of 19,600 families with two children (you will understand why I've chosen this seemingly random number in a moment). Of those families, suppose they are evenly divided among boy boy, boy girl, girl boy, and girl girl households. In particular, we see that there are 4,900 families with two boys, 4,900 families with two girls, and 9,800 families with a boy and a girl (in half of these families the boy is older, and in half the boy is younger).
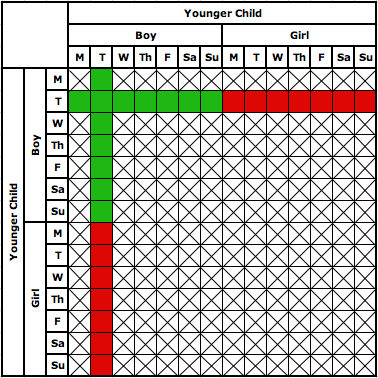
Now suppose we further subdivide the data according to the day of the week in which the child was born. Suppose that a child is equally likely to have been born on any day of the week. This means that, for example, among the 4,900 families with two boys, 4,900 ÷ 49 = 100 will have boys who were both born on Monday, 100 will have boys for which the oldest was born on Monday and the youngest Tuesday, 100 will have boys for which the oldest was born on Monday and the youngest Wednesday, and so on. In other words, for every possible combination of sexes and days of birth, there will be 100 families that match that combination.
Suppose, now, that you take a random family in which one of the children is a boy born on Tuesday. There will be 1,400 families for which the younger child is a born boy on Tuesday, and 1,400 families for which the older child is a boy born on Tuesday, which means there are 2,700 families total families under consideration (note that we have counted the 100 families with two boys born on Tuesday twice). Of those 2,700 families, 1,300 will have two boys, for the same reason as above (you can also look at the diagram above - imagine each square as representing 100 families in the survey). So, if we pick a FAMILY at random with a boy born on Tuesday, the probability that the other child is a boy is 1,300 out of 2,700, or 13/27.
Now, instead of picking a family at random, suppose we pick a BOY at random who was born on Tuesday, and ask for the probability that the boy's sibling is also a boy. In this case, note that there are 2,800 boys in our sample who were born on Tuesday - 1,400 who are the younger sibling and 1,400 who are the older sibling. In particular, note that we don't subtract out the families with two boys both born on Tuesday for double counting in this case; this is because we are choosing the boy, not the family, and choosing the younger boy born on Tuesday is different from choosing the older boy born on Tuesday. Because there's nothing to subtract out, we see that of these 2,800 boys, 1,400 have sisters and 1,400 have brothers. Therefore the probability that the BOY has a brother is 1/2, the answer our intuition gave us from the beginning!
In other words, you can try to understand this seeming paradox as a difference in perspective. If we look from the perspective of the family unit, the probability that a two-child FAMILY with one son born on Tuesday will have two sons is 13/27, slightly less than one half. However, from the perspective of the children, the probability that a BOY born on Tuesday in a two-child family will have a brother as opposed to a sister is 1/2. In this latter case, the day of the week really is irrelevant.
For some, however, this explanation still may not seem like enough. I'd encourage anyone with a different approach to sound off below!
Psst ... did you know I have a brand new website full of interactive stories? You can check it out here!
comments powered by Disqus