Football Pools, Part 3
This is the third in a series of posts about pools used for betting on the outcome of football games (part one can be found here, and part two here). Let me briefly recall the setting, which is probably familiar to anyone who has been to a Super Bowl party. Typically, one bets on the outcome of a football game using a 10 x 10 grid. People can buy any number of the 100 squares on the grid, and when all the squares have been purchased, each row and each column is assigned a random digit from 0 to 9.
Suppose, for example, that you buy four squares, and after the rows and columns have been labeled, you find that you own square 3-7, square 2-5, square 9-0, and square 6-6. You will win money if, at the end of any one of the four quarters, the last digit in each team's score matches your pair. For example, if the score after the 3rd quarter is 13-27, you will win some money, since the last two digits are 3 and 7, and you own square 3-7. There are variants of this: some pools only pay out every half, not every quarter, and usually the payouts vary by quarter, so that having the right square at the end of the game wins you more money than having the right square at the end of the first quarter.
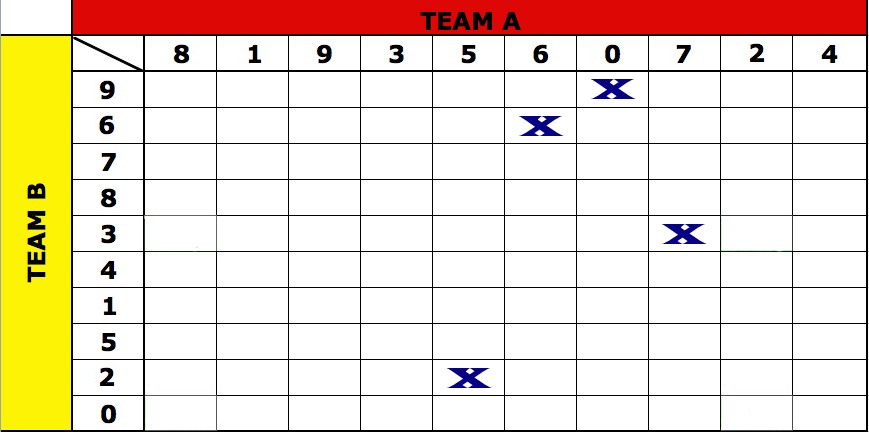
Here's an example of a football pool which has been tagged in the four squares mentioned above.
In the first part of this discussion, we introduced a new way to conduct the pool: rather than looking at the last digit of a team's score, we looked instead at the digital root of the team's score. Recall that the digital root of a team's score is obtained by adding the digits in their score. If that sum is between 1 and 9, we stop - if it is larger than 9, we compute the digital root again, until we get a digit between 1 and 9. For example, the digital root of 14 is 1 + 4 = 5, while the digital root of 38 is 2, since 3 + 8 = 11, and 1 + 1 = 2. We then analyzed the distribution of scores, and found that the digital root of a team's score is more evenly distributed between 1 and 9 than the last digit of a team's score is evenly distributed between 0 and 9 (this is subject to the convention that we assign 0 a digital root of 9, since 0 is the only number with digital root equal to 0).
In the second part of the discussion, we tackled questions of independence. Namely, we asked whether the last digit in one team's score is independent of the last digit of the other team's score, and similarly we asked whether the digital root in one team's score is independent of the digital root of the other team's score. In both cases, we found the answer to be negative.
The subject of this article is based on the following observation: when you have wagered in a traditional football pool, it's not uncommon for a small number of squares to be hit with high frequency during the course of a game. For example, suppose you watch a game in which one team scores 7 points, then 3, then 7, then 3, while the opposing team never scores. This means that the game's score will go from 0-0, to 7-0, to 10-0, and then to 17-0. So, while there are four unique scores in the game, with the usual football pool, only two squares will be hit: the 0-0 square, and the 7-0 square. However, with the digital root pool, four squares will be hit: again using the convention that we assign 0 a digital root of 9, the squares will be 9-9, 7-9, 1-9, and 8-9.
The reason the digital root pool hits more squares in this case is because whenever one team increases its score by 10, the last digit of their score will return to a previous value. However, with the digital root method, if a team increases its score by 10, the digital root increases by 1. Because a score increase of 10 is a relatively common occurrence in football (all one needs is a touchdown, extra point, and field goal), one may therefore guess that using the digital root pool, more squares should be hit during the course of the game.
Whether one would want more squares to be hit or not is up for debate, but I see certain benefits. For example, if more squares are hit during the game, then more people will have something invested in the game as it airs. If you are sitting on the square that represents the current score, you want the score to remain the same through the end of the quarter so that you can reap the rewards - but if the winning squares keep bouncing around between a small number of people, there may be fewer people actively interested in the score as the game progresses. This is especially true in Super Bowl parties, when many of the attendees are less interested in the game than they should be.
In other words, I'm of the belief that if more squares are hit, it's a good thing. It therefore becomes natural to ask whether or not the digital root pool actually does hit more unique squares than the traditional pool. Thankfully, we have a wealth of data which we can use to answer this question.
I looked at all the games from this current season, and counted the number of boxes that would have been hit in each game using the traditional pool and the digital root pool. Averaged over 331 games (this includes preseason and postseason), the number of squares hit using the traditional pool is approximately 6.84. By comparison, the number of squares hit using the digital root pool is 8.43 - an increase of 1.59 boxes, or an increase of about 23%. This effect is amplified when one considers the fact that the digital root pool uses only 81 squares, as opposed to the traditional pool's 100. This means that as a proportion of the total number of squares, the traditional pool hits about 6.84% of its squares, while the digital root pool hits 10.4% - here we have an increase of over 50%!
This is strong evidence that the digital root pool hits more squares than the tradition pool. In fact, the data shows that an average game will have a change in the score approximately 8.73 times, which is only a bit higher than the average number of boxes hit by the digital root pool. This makes sense when we slice the data another way: of the 331 games analyzed, in 252 of them the number of squares hit with the digital root pool was equal to the number of changes of score, meaning that no square got hit more than once. The same cannot be said of the traditional pool - in this case, the number of games in which no square got hit more than once was only 62.
The data has convinced me that the digital root pool may be better suited for festive gathering, where wagering on football will be but one of many activities designed to induce merriment. At the very least, it's hard to argue that the traditional pool will hit as many squares as the digital root pool. Some may balk at a break from football pool tradition, but that's ok. I won't watch football games with them anyway.
Psst ... did you know I have a brand new website full of interactive stories? You can check it out here!
comments powered by Disqus
